Chapt 5 overview + additional resources

Center of Mass Youtubes:

Just for fun - MIT Physics Demo -- Center of Mass Trajectory

Centroid

Kahn Academy - Center of Mass

Finding resultants of distributed beam loading conditions.

 Fluid Mechanics: Introduction to Forces on Planar and Submerged Surfaces

Fluid Mechanics: Forces on Curved Surfaces: Example 1

https://www.youtube.com/watch?v=E8EQ8uYMB88 

 https://www.youtube.com/watch?v=-adMiG0hyBM

centroid of the volume obtained by rotating the shaded area about the x-axis

Quiz:
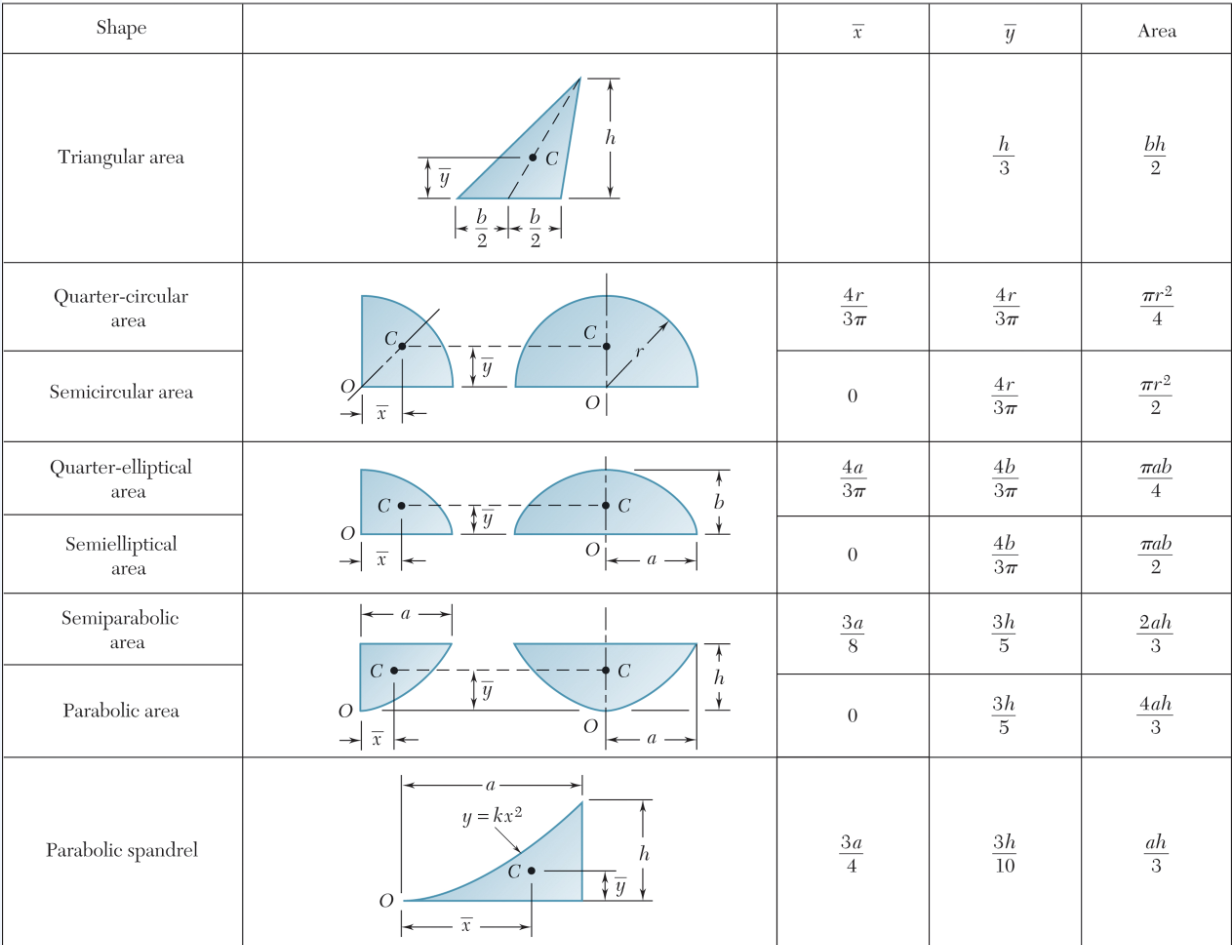
1.  Locate the centroid of the plane area (similar to problems 5.1-5.16)
2.  For a given Distributed load, find a) the magnitude and location of the resultant, b) reactions at supports.  (similar to problems 5.66-5.95)
3.)  Locate the center of gravity for a 3D object (similar to problems 5.96-5.121)
Extra Credit: Locate the centroid of a volume created by rotating an area about an axis. (similar to problems 5.125-5.129)

5.10Centroids of Volumes, 5.11 composite Bodies, 5.12 Volumes by Integration

Examples:

HW:

 y=-(2h^2-3b^2)/(2(4h-3b))

 x=0.1402, y=0.0944, z=0.0959

 x=0.410, y=0.510, z=0.15

y=0, z=0, x=2.34

5.8 Loads on Beams 5.9 Forces on Submerged surfaces

Example:

 

 

 

Examples:

 

HW

 

 

 

 

5.6-5.7 Centroids by integration & Pappus-Guldinus

Example:  Find the centroid of a triangle:

https://www.youtube.com/watch?v=Wg79PFCV2m8

I want this to be a statics class, not a math class, so you can use:

http://integrals.wolfram.com/index.jsp

Example:

Volume of Sphere from rotating semicircle around axis.

Use: http://en.wikipedia.org/wiki/List_of_centroids

(Circumference of a circle = 2*Pi*r)

Surface area of sphere:

5.8b:








Examples:

HW:

y=x=9a/20

x=(2/5)L, y=(12/25)h

V=31.91

Chapter 5.1-5.5: Distributed Forces: Centroids and Centers of Gravity

Statics Lecture 29: Center of Gravity

Statics Lecture 30: Centroid of an Area

Statics Lecture 31: Centroid of composite areas

Statics Lecture 32: Mass Moment of Inertia and Area Moment of Inertia

 

 Statics Lecture 33: Area Moment of Inertia -- Calculation

Statics Lecture 34: Area Moment of Inertia -- Composite Areas

wiki list of centroids:

http://en.wikipedia.org/wiki/List_of_centroids

http://www.engineering.com/Library/ArticlesPage/tabid/85/articleType/ArticleView/articleId/109/Centroids-of-Common-Shapes.aspx

centroids:

http://en.wikipedia.org/wiki/Centroid

 

5.2: Start in 2D

Divide plate into n small elements, each with weight "W".

element n = 1 (x1, y1)

element n = 2 (x2, y2) etc.

Total weight:

Moments about x and y axis:

 or: 

Center of Gravity of a wire:

** Center of gravity "G" is not usually located on the wire.

Similar to:


Just divide above by thickness and specific weight:

Centroid of an Area
Define coordinates for the center of gravity of a homogeneous plate:

For homogeneous wire:

5.4  First Moments of Areas and Lines

   

Symmetrical objects:

5.5  Composite Plates and Wires

 1st moment of composite area:

Pay attention to your signs!

Probs 5.1-5.33

Examples:

Find the centroids of the areas:

HW Problems:

x=19.27, y=26.6

x=92, y=23.3

x=3.2, y=2.0

56.7°