Watching someone else do something?
Or doing it yourself?
.

.
Which part would you rather do in class
- the watching part (lecture)?
- or the doing part (solving problems)?
Homework:
We'll be using the lectures by Yiheng Wang, now teaching ENGR at LSC Cy-Fair, throughout the semester. These are a great resource, are very clear and concise, so bookmark her page! Through watching lectures at home, we will have more time to work through examples problems and do HW in class.
Another statics resource:
https://ecourses.ou.edu/cgi-bin/display_lectures.cgi?course=st&status=disp_ch
Read Chapter 2 in book
To motivate you to do your homework...
- Beginning of class 10 minute study comprehension quiz.

.
2.1-2.3: Vocabulary~~~~~~~~~~~~~~~~~~~~~~~
resultant force
- replacing multiple forces acting on a particle with a single equivalent force
- Make a parallelogram,
- resultant = diagonal of parallelogram
note: the magnitude of the vector
P + Q is NOT equal to the sum of the magnitudes o P+Q.
equilibrium
particle

force
Vector quantity
action of one body on another; characterized by:
action of one body on another; characterized by:
- point of application
- magnitude
- SI units: 1,000N = 1 kN
- U.S. customary: 1,000 lb = 1 kip
- Direction of Force
- line of action - line force acts along
- sense: arrow pointing which way it is acting; ↑? ↓?
Scalar
- has magnitude but not direction.
- Examples:
- mass,
- volume,
- temperature
Vector
- has magnitude and direction
- add according to the parallelogram law.
- Examples:
- displacements
- velocities
- accelerations
Vector
classifications
- Fixed or bound vectors
- Free vectors
- Sliding vectors
2.4 Addition of vectors~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Trapezoid rule for vector addition
Trapezoid rule for vector addition
Triangle
rule for vector addition
- Just draw half of the parallelogram
- arrange vectors head to tail
- Just draw half of the parallelogram
- arrange vectors head to tail
Sum of three or more vectors
Add two together, and then add on the third etc.
P + Q + S = (P + Q) + S

It doesn't matter what order you add them
Product of a Scalar and a Vector
- Keep the same line of action
- Change the magnitude
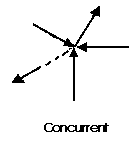
concurrent forces
all forces pass through a common point
Resultant of concurrent forces:
Replace multiple forces with single force,
.
R → same effect as S+P+Q on "A"
Resolution of a force into components
Describe force in terms of x, y, z
Trig Review~~~~~~~~~~~~~~~~~~~~~~~~~~.
Law of cosines
Law of sines
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Group Exercise:
2.16 hint - do not assume that R is perfectly horizontal!!
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
2.7
Rectangular Components of a Force: Unit Vectors
rectangular vector components

..
unit vectors
scalar components Fx and Fy

.
2.8 Addition of Forces by Summing Components
Trig Review
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Class Exercise
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
*******************************************************************
HW2:
2.6, 2.15, 2.30, 2.33,
********************************
2.9 Equilibrium of a Particleequilibrium
resultant of all forces acting on a particle is zero
Newton’s First Law
If the resultant force on a particle is zero, the particle will remain at rest or will continue at constant speed in a straight line
2.11
Free-Body Diagrams
Space
Diagram
A sketch or picture of the problem

Free Body Diagram FBD
sketch showing the forces on a selected particle

Free Body Diagram FBD
sketch showing the forces on a selected particle

class exercise:
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
see pg 47 in your book
See example problem 2.7 in your book - pg51~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
HW#3:
2.46, 2.51, 2.72, 2.89
ΣFx = 0
ΣFy = 0
ΣFz = 0
Study sample problem 2.9 in book
Class Problems:
2.103
2.108
HW: 2.104, 2.107































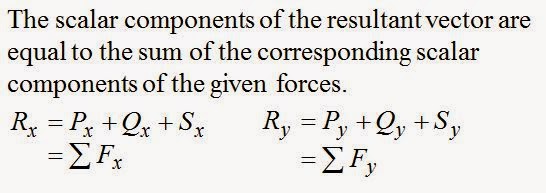




























No comments:
Post a Comment